Yesterday I disabused myself of the nothing that it would be easy to to manipulate vertices of a plane in order to make blocks and steps. I had hoped to use this technique in order to build Minecraft-like landscapes, but that turns out not to work.
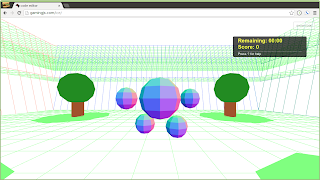
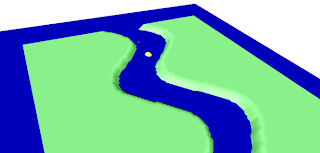
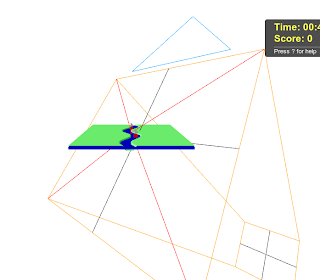
I had originally tried a high resolution geometry to build the steps:
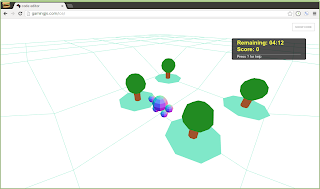
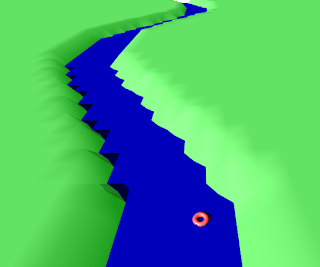
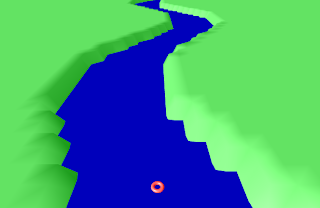
But I noticed a subtle sloping of the steps. I had hoped that simplifying the number of faces (from 100 to 10 in each direction) would help:
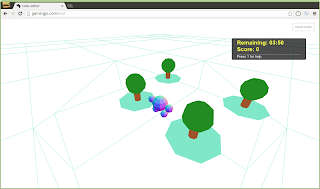
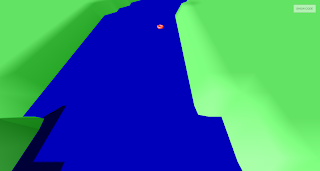
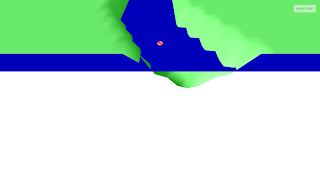
It did help. It became easier to see the confused vertices that I was causing when I tried to shift the vertices in an attempt to make the steps flat:
I am still not 100% clear on what is going wrong with those seemingly diagonal face edges. It occurs to me that I was headed in the right direction with simplifying the problem, but that I might need to simplify a bit more—and with a bit more deliberation.
So I break the plane into a 5 by 5 grid of faces:
var ground = new THREE.Mesh(
new THREE.PlaneGeometry(10000, 10000, 5, 5),
new THREE.MeshNormalMaterial()
);
That also helps me to realize that of course this does not work. If I “unfold” the sides and bottom of a cube, it would look like:
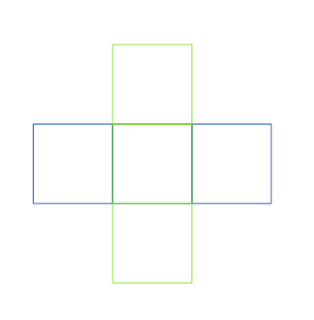
Fold that along the lines and you have a box. Unfortunately, I do not have this. I have the entire 3×3 grid and there is no way to fold just the middle squares:

Actually...
If I fold up the middle vertices, I would have a cube that also had vertices still at the corners (on the “floor”). But nothing is stopping me from moving the corner vertex up as well. Another way to build a cube would be to move the center vertices out to the edges (leaving a 1×1 square) and then pushing down the center vertices
Back in my 5×5 grid, this means shifting the third and fourth rows and columns out to the same position as the second and fifth columns:
var faces = 5;
var ground = new THREE.Mesh(
new THREE.PlaneGeometry(10000, 10000, faces, faces),
new THREE.MeshNormalMaterial()
);
ground.rotation.x = -Math.PI/2;
var vertices = ground.geometry.vertices;
for (var i=0; i<=faces; i++) {
// The third row of vertices should have same Y as the second
vertices[2*(faces+1) + i].y = vertices[1*(faces+1) + i].y;
// The fourth row of vertices should have same Y as the fifth
vertices[3*(faces+1) + i].y = vertices[4*(faces+1) + i].y;
// The third column of vertices should have same X as the second
vertices[i*(faces+1) + 2].x = vertices[i*(faces+1) + 1].x;
// The fourth column of vertices should have same X as the fifth
vertices[i*(faces+1) + 3].x = vertices[i*(faces+1) + 4].x;
}
I am glad to have sussed that one out. I still lack some of the innate 3D spatial visualization that would help me understand when I am doing something silly. Hopefully this exercise will prove to be of some help with that.
There is no way that the above explanation would work in 3D Game Programming for Kids. This is not a huge deal as I had already not planned on covering this topic in the book. Still, it might be worth another day of play to see if I can tease out a better way of explaining this.
Tomorrow.
Day #708